WRITING TIPS LESSON
COMMA CONFIDENCE: COMMAS IN COMPOUND SENTENCES
KEYS TO SUCCESS
Three keys are needed to master the comma rule for compound sentences. The first key is correctly identifying a compound sentence. The second key is correctly identifying conjunctions.The third key is identifying the punctuation patterns of compound sentences.
Key #1: Identify a Compound Sentence

The key to identifying a compound sentence is to know these three basic parts of speech: subject, verb, and object. Put these together and you have an independent clause with this pattern: SVO. A compound sentence contains two or more independent clauses. Thus to locate a compound sentence, you look for this pattern: SVO, and SVO. In this case, the two independent clauses are joined with a comma and coordinating conjunction (more on this in Key #2). This is the most common compound sentence pattern, but we must remember that other patterns exist. When you know the patterns of compound sentences, you know when to use a comma. .
Notice that in the SVO pattern an independent clause is the same as a simple sentence, a complete thought. Simple sentences must have at least a verb with an implied subject, and that pattern is V (Example: Jump! = [You] jump) . Sometimes simple sentences have only a subject and a verb, and that pattern is SV (Example: Harry jumped!). The most frequent pattern, however is SVO, and we are defining object (O) as anything that comes after the verb (Harry jumped into the air!) such as a prepositional phrase, a noun phrase, a simple object, etc..Native English speakers can usually test for an independent clause by reading it aloud. If it sounds like a complete thought, it usually is.
These examples should help you recognize the basic sentence patterns that we need to recognize compound sentences:
Notice that in the SVO pattern an independent clause is the same as a simple sentence, a complete thought. Simple sentences must have at least a verb with an implied subject, and that pattern is V (Example: Jump! = [You] jump) . Sometimes simple sentences have only a subject and a verb, and that pattern is SV (Example: Harry jumped!). The most frequent pattern, however is SVO, and we are defining object (O) as anything that comes after the verb (Harry jumped into the air!) such as a prepositional phrase, a noun phrase, a simple object, etc..Native English speakers can usually test for an independent clause by reading it aloud. If it sounds like a complete thought, it usually is.
These examples should help you recognize the basic sentence patterns that we need to recognize compound sentences:
EXAMPLE: SIMPLE SENTENCE (INDEPENDENT CLAUSE)

EXAMPLE: SIMPLE SENTENCES DO NOT HAVE TO BE SHORT
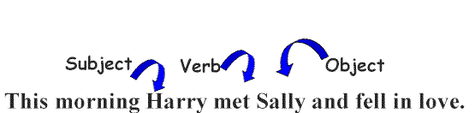
Even if we add words to the object, we do not necessarily change the basic SVO structure of a simple sentence.
EXAMPLE: PUTTING TWO SIMPLE SENTENCES TOGETHER CREATES A COMPOUND SENTENCE.
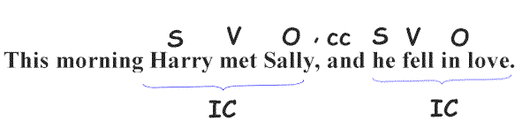
Put these words together with another simple sentence and you do change the basic structure. With two independent clauses (IC), you have a compound sentence: SVO, and SVO.
Look again: Notice that the pronoun, he, is a subject of an independent clause. Adding this subject turned what was an object phrase into an independent clause.
Notice the pattern. SVO [something] SVO. Next we examine what that something-in-the-middle can be.
Look again: Notice that the pronoun, he, is a subject of an independent clause. Adding this subject turned what was an object phrase into an independent clause.
Notice the pattern. SVO [something] SVO. Next we examine what that something-in-the-middle can be.
